In my first blog, I reviewed the background of HMM model in speech recognition. At the time of writing that blog, I still didn’t fully understand how the last step, the decoding step, works. Recently I read a textbook named speech and language processing written by Daniel Jurafsky and James H. Martin. The Chapter 9 Automatic Speech Recognition really helped me a lot in understanding the decoding step. In this blog I am going to write what I have learned.

Hierarchy of phones, words and sentences

After converting original audio wavefile to features, we have a sequence $(f_1, \ldots, f_T)$. The goal is to find a sequence of words $(w_1, \ldots, w_N)$ that matches the feature sequence best.

In my previous blog, I have learned that people have been using HMM to model basic units (phones) in speech. To bridge the gap between word decoding and phone level HMMs, let’s look at the hierarchical structure of HMM states, phones, words and sentences.

A phone is usually modeled by a HMM with three states. ¹. The three states correspond to three subphones, which are transition-in, steady-state, transition-out regions of the phone.

A word is consisted by a sequence of phones. For example, “one” is composed of three phones: “w”, “ah” and “n”. The word model is just the sequential concatenation of the phone models.

Lexicon contains information about phone sequence of words. There is a dictionary (lexicon) which includes phone sequence for each of word. Therefore once all phones are represented by pre-trained HMM models, the word models become available by searching in the dictionary and concatenating phone level models belonging to that word. Compared with fitting a HMM for individual word, this strategy greatly reduced the complexity.

A sentence is a grammatically valid sequence of words. Words do not randomly connect to form a sentence. The transition between adjacent words can be estimated from a large text corpus.

Combine all together

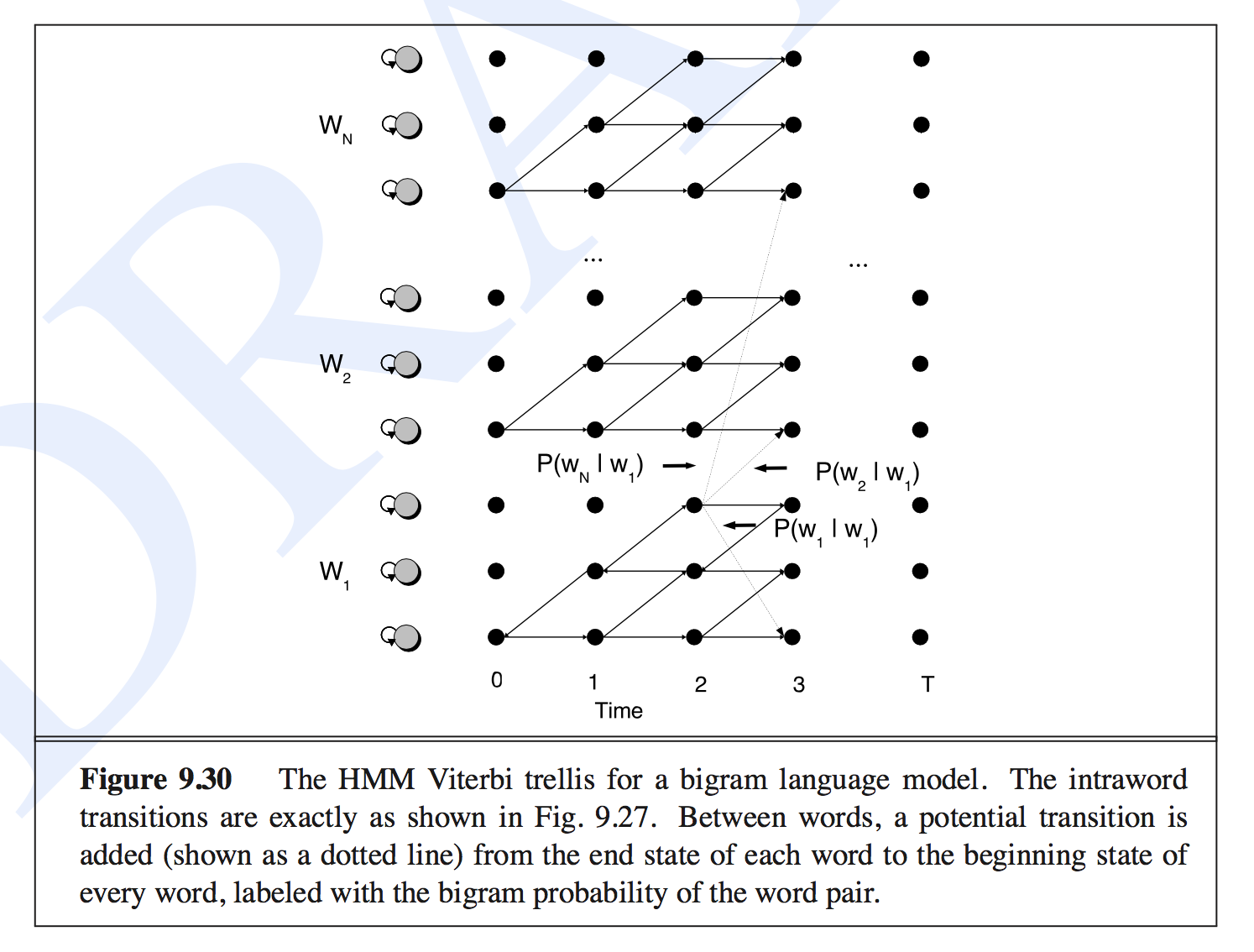
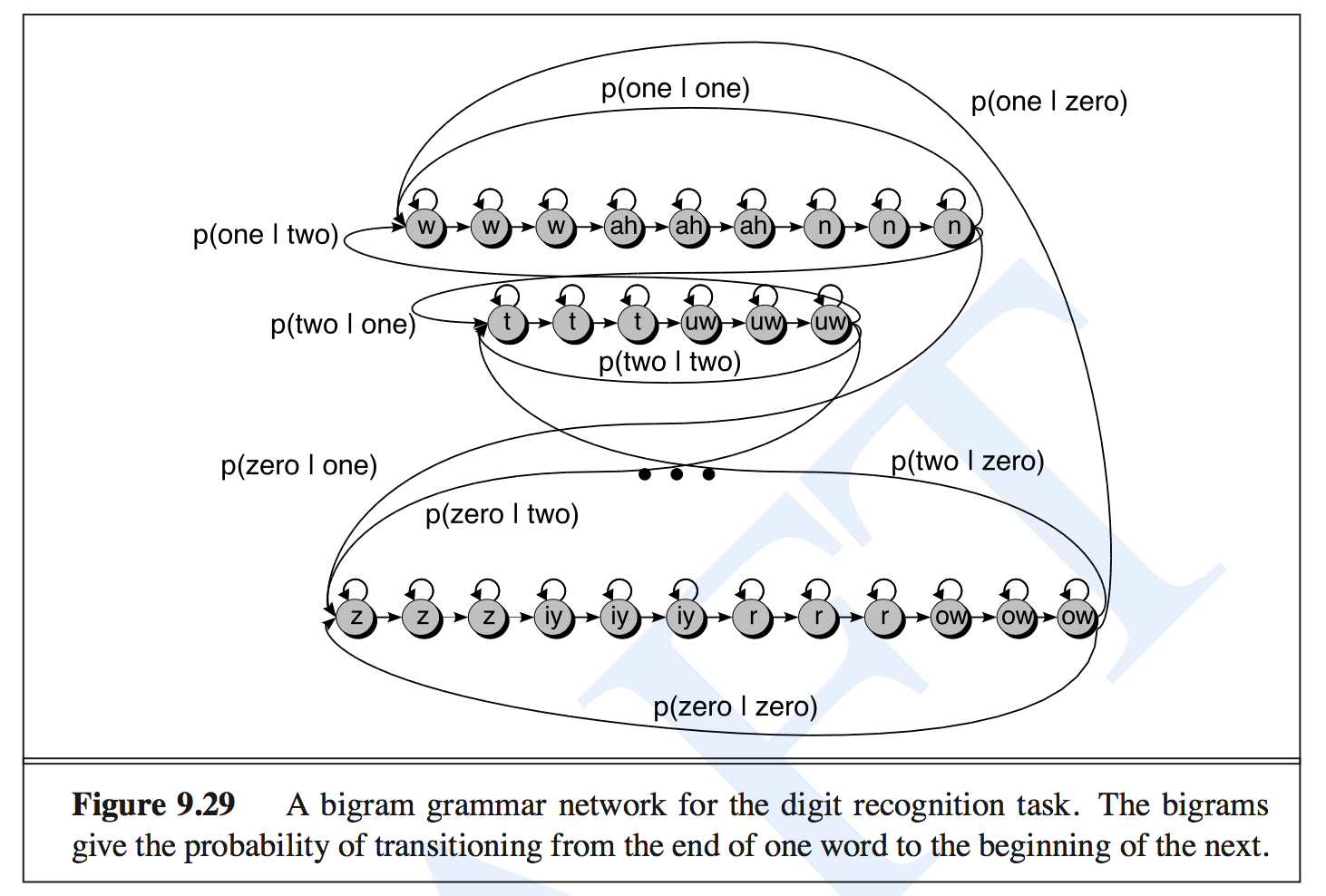
Let’s put together what we have learned in a simple digit recognition task. The words are the digits from one to nine. Following figure from ¹ shows the hierarchical transitions of this task. $p(one | two)$ represents the transition probability from digit two to one.

Given this hierarchical transition matrix, a Viterbi trellis decoding method is used. Following figure from ¹ shows the scheme of this decoding process. The words (digits) are stacked vertically and the feature sequence is shown horizontally.